Metode Elbow dalam Algoritma Klastering untuk Memilih Jumlah Klaster Optimal

Pada algoritma klastering, penentuan jumlah klaster yang tepat (nilai K) merupakan langkah penting. Salah satu metode yang sering digunakan untuk menemukan jumlah klaster yang optimal adalah metode Elbow.

Sebelum mempelajari materi tentang Metode Elbow dalam Algoritma Klastering untuk Memilih Jumlah Klaster Optimal, terlebih dahulu pelajari materi tentang: Contoh Perangkat Output Komputer yang Membantu Produktivitas, Algoritma K-Means dan Implementasinya, dan Algoritma Klastering dan Penggalian Pola dari Kumpulan Data.

Pengertian Metode Elbow

Metode Elbow adalah teknik yang digunakan untuk menemukan jumlah klaster yang optimal dalam algoritma klastering, khususnya pada algoritma K-Means. Ide dasarnya adalah dengan mengamati penurunan varians dalam setiap klaster terhadap jumlah klaster yang berbeda. Grafik yang menampilkan nilai varians sebagai fungsi dari jumlah klaster akan memiliki bentuk seperti "siku" (elbow). Titik pada siku tersebut merupakan indikasi bahwa penambahan klaster setelahnya memberikan penurunan yang kurang signifikan dalam varians.

Langkah-langkah Menggunakan Metode Elbow:

• Membuat Model K-Means: Mulailah dengan membuat model K-Means dengan berbagai nilai K yang mungkin, misalnya dari 1 hingga N (jumlah maksimum klaster yang diizinkan).
• Melakukan Klastering: Gunakan model K-Means untuk melakukan klastering pada data yang relevan.
• Menghitung Varians dalam Setiap Klaster: Hitung varians (dalam K-Means, ini sering kali adalah inersia atau inertia_) dari setiap klaster yang dihasilkan oleh model.
• Membuat Plot Varians vs. Jumlah Klaster: Buatlah grafik yang menampilkan nilai varians sebagai fungsi dari jumlah klaster (nilai K).
• Identifikasi Titik Elbow (Siku): Amati grafik yang dihasilkan. Cari titik di mana penambahan klaster setelahnya tidak memberikan penurunan varians yang signifikan. Titik ini mirip dengan siku (elbow) pada grafik.
• Pemilihan Jumlah Klaster: Pilih nilai K di titik siku tersebut sebagai jumlah klaster yang optimal.

Contoh soal dan jawaban yang menggunakan metode Elbow untuk menentukan jumlah klaster yang optimal dalam algoritma klastering.

Contoh Soal:

Sebuah perusahaan ingin menganalisis data penjualan produk untuk memahami perilaku pembeli berdasarkan dua fitur utama: jumlah produk yang dibeli (Quantity) dan total biaya pembelian (TotalCost). Perusahaan tersebut ingin menggunakan algoritma K-Means untuk mengelompokkan pembeli ke dalam klaster berdasarkan perilaku pembelian. Diberikan dataset pembelian dengan 200 entri pembeli.

Berikut adalah beberapa langkah yang dilakukan:

1. Lakukan klastering pada data dengan menggunakan algoritma K-Means dengan nilai K yang bervariasi dari 1 hingga 10.
2. Hitung nilai inersia (inertia) untuk setiap nilai K.
3. Gunakan metode Elbow untuk menentukan jumlah klaster yang optimal berdasarkan grafik inersia vs. jumlah klaster.

Jawaban:

Setelah melakukan analisis terhadap data penjualan, berikut adalah hasil perhitungan inersia untuk nilai K dari 1 hingga 10:

• Nilai K = 1, Inersia = 326541.2
• Nilai K = 2, Inersia = 212455.3
• Nilai K = 3, Inersia = 128972.5
• Nilai K = 4, Inersia = 87563.6
• Nilai K = 5, Inersia = 56784.2
• Nilai K = 6, Inersia = 39871.7
• Nilai K = 7, Inersia = 28523.9
• Nilai K = 8, Inersia = 21648.6
• Nilai K = 9, Inersia = 17659.2
• Nilai K = 10, Inersia = 14560.1

Gambar 1: Grafik Inersia VS Jumlah Klaster

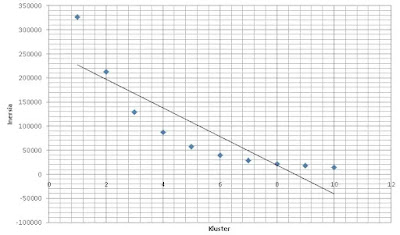
Dari hasil perhitungan, data dapat diubah dalam bentuk visualisasi grafik inersia vs jumlah klaster seperti diperlihatkan pada Gambar 1.

Dari grafik yang dihasilkan, terlihat bahwa terdapat titik siku (elbow) yang jelas pada nilai K=3. Setelah nilai K=3, penurunan inersia tidak lagi signifikan. Oleh karena itu, berdasarkan metode Elbow, jumlah klaster yang optimal untuk data ini adalah 3.

Kesimpulan:
Dalam contoh ini, menggunakan metode Elbow pada algoritma K-Means membantu perusahaan untuk menentukan jumlah klaster yang optimal untuk mengelompokkan pembeli berdasarkan perilaku pembelian. Dengan mengetahui jumlah klaster yang tepat, perusahaan dapat memahami pola pembelian pelanggan secara lebih baik dan menyesuaikan strategi pemasaran atau layanan untuk setiap kelompok pelanggan dengan lebih efektif.

Baca Juga:

• Memahami Metode Silhouette Score dalam Analisis Klastering
• Algoritma Hierarchical Clustering Tentang Pemahaman Pengelompokkan Data Bertingkat
• Manfaat Air Rebusan Daun Sirih yang Membuatnya Sebagai Ramuan Tradisional Berharga
• Mengapa Jepang Sering Mengalami Gempa Bumi

Informasi Tambahan

Untuk menghitung nilai inersia dalam algoritma K-Means, langkah-langkahnya adalah sebagai berikut:

1. Setelah klastering dilakukan dengan menggunakan algoritma K-Means dan nilai K tertentu, maka didapatkan nilai pusat klaster (centroid) untuk setiap klaster.
2. Hitung jarak kuadrat dari setiap titik data di dalam klaster terhadap pusat klasternya (centroid). Misalnya, jika Xi adalah titik data dan Cj adalah pusat klaster untuk klaster j, maka jarak kuadratnya adalah  ${\sum }_{�=1}^{�}({�}_{�}-{�}_{�}{)}^2$. 
3. Lakukan perhitungan jarak kuadrat untuk semua titik data di dalam semua klaster.
4. Jumlahkan semua jarak kuadrat ini untuk mendapatkan nilai inersia total dari klasterisasi.

Contoh perhitungan nilai inersia untuk sebuah set data dengan tiga klaster. Asumsikan terdapat tiga klaster dengan pusat klaster (centroid) sebagai berikut:

• Klaster 1: Pusat klaster = (2, 3)
• Klaster 2: Pusat klaster = (5, 7)
• Klaster 3: Pusat klaster = (9, 2)

Hitung nilai inersia untuk setiap klaster dengan beberapa titik data secara sederhana.

Langkah 1: Pusat Klaster

Pusat klaster untuk setiap klaster sudah diketahui:

• Klaster 1: Pusat klaster (centroid) = (2, 3)
• Klaster 2: Pusat klaster (centroid) = (5, 7)
• Klaster 3: Pusat klaster (centroid) = (9, 2)

Langkah 2: Data Tiap Klaster

Misalkan memiliki titik data di dalam klaster sebagai berikut:

• Klaster 1: Data = (1, 2), (3, 4)
• Klaster 2: Data = (4, 6), (6, 8), (5, 5)
• Klaster 3: Data = (8, 1), (9, 3), (10, 2)

Selanjutnya akan dihitung jarak kuadrat dari setiap titik data di dalam klaster terhadap pusat klasternya, dan kemudian menjumlahkannya untuk mendapatkan nilai inersia.

Langkah 3: Perhitungan Jarak Kuadrat

Klaster 1:

• Jarak kuadrat dari (1, 2) ke (2, 3) = (1 − 2)² + (2 − 3)² = 1 + 1 = 2
• Jarak kuadrat dari (3, 4) ke (2, 3) = (3 − 2)² + (4 − 3)² = 1 + 1 = 2
• Total inersia untuk Klaster 1 =  2+ 2 = 4

Klaster 2:

• Jarak kuadrat dari (4, 6) ke (5, 7) = (4 − 5)² + (6 − 7)² = 1 + 1 = 2
• Jarak kuadrat dari (6, 8) ke (5, 7) = (6 − 5)² + (8 − 7)² = 1 + 1 = 2
• Jarak kuadrat dari (5, 5) ke (5, 7) = (5 − 5)² + (5 − 7)² = 0 + 4 = 4
• Total inersia untuk Klaster 2 = 2 + 2 + 4 = 8

Klaster 3:

• Jarak kuadrat dari (8, 1) ke (9, 2) = (8 − 9)² + (1 − 2)² = 1 + 1 = 2
• Jarak kuadrat dari (9, 3) ke (9, 2) = (9 − 9)² + (3 − 2)² = 0 + 1 = 1
• Jarak kuadrat dari (10, 2) ke (9, 2) = (10 − 9)² + (2 − 2)² = 1 + 0 = 1
• Total inersia untuk Klaster 3 = 2 + 1 + 1 = 4

Langkah 4: Hitung Total Inersia

Jumlahkan nilai inersia dari setiap klaster untuk mendapatkan nilai inersia total:

• Total inersia = Inersia Klaster 1 + Inersia Klaster 2 + Inersia Klaster 3 = 4+8+4=16

Jadi, nilai inersia total untuk dataset ini dengan tiga klaster adalah 16.

Keuntungan Metode Elbow

• Visualisasi yang Sederhana: Metode Elbow menyediakan visualisasi yang mudah dipahami untuk menentukan jumlah klaster yang optimal.
• Pemilihan Jumlah Klaster yang Subyektif: Dengan melihat grafik, pengguna dapat membuat keputusan yang lebih baik secara subyektif dalam pemilihan nilai K.

Keterbatasan Metode Elbow:

• Kurang Tepat dalam Kasus Kompleks: Pada beberapa kasus data yang kompleks, grafik mungkin tidak menunjukkan siku yang jelas, membuat penentuan jumlah klaster yang optimal menjadi sulit.

Metode Elbow adalah alat yang berguna dalam menentukan jumlah klaster yang optimal dalam algoritma klastering, terutama dalam algoritma K-Means. Meskipun tidak selalu memberikan solusi yang pasti, metode ini memberikan pandangan visual yang bermanfaat dalam pemilihan nilai K yang dapat digunakan untuk membantu dalam analisis data yang lebih baik dan relevan.

Referensi Tambahan:

• Ciri Kurikulum Merdeka Belajar dan Penjelasannya
• Mengapa Toleransi Sangat Penting Bagi Keberagaman Bangsa Indonesia
• Masa Pubertas dan Pencarian Identitas Diri
• Definisi Kecerdasan dan Penjelasannya
• Teori Kecerdasan Ganda dan Penjelasannya
• Komponen Kecerdasan Emosional dan Penjelasannya
• Konsep Intelligence Quotient dan Kategorinya

Artikel ini didedikasikan kepada: Yudha Harizky Santoso, Yusria Ikhsanika Jannah, Yusrina Fisabila Izza, Zahrafi Surya Masdifa, dan Zahro Atira Kholida.

Location: Kota Semarang, Jawa Tengah, Indonesia

Berbagi :